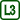Collection of Physics Experiments

Diffraction on a CD

Experiment number : 1704

• Goal of experiment

  This experiment shows that a CD has the characteristics of an optical grating. When demonstrating this experiment we can perform measurements and calculate the wavelength of the laser or the grating constant.

• Theory

  Diffraction (bending) of light is due to wave properties of light. It means that when a light wave encounters an obstacle, it does not propagate linearly behind the obstacle. During diffraction on an optical grating, formed by a system of a large number of parallel slits with equal width, a monochromatic light wave of a wavelength λ creates an interference pattern on a screen. The directions of interference amplification are determined by the angle α, for which it applies

  \[b \sin⁡α=kλ\tag{1}\]

  where \(b \) is the distance between two adjacent slits, called a grating constant or a grating period, and k = 0, 1, 2, … is the order of diffraction.

  A recording on a CD is in the form of microscopic pits of different lengths that carry the information. These pits are placed in rows of the same width and equal distance, which form a diffraction grating on the mirror surface of the CD.

• Tools

  Laser pointer, compact disc in a plastic box, thick paper, scissors, mat, ruler, pencil.

• Procedure

  1. We cut a hole in the paper and insert the laser pointer in it. A good option is a hole horizontally in the middle and at a height of six centimetres vertically.
  2. We place an open box with the CD in it with the recording side facing out on the mat.
  3. In the distance l = 25 cm from the disk we place the paper with the laser pointer; the paper is parallel to the CD
  4. We point the laser beam approximately in the middle of the CD recording.
  5. On the paper we can now observe the beam directly reflected from the disk surface and slightly less clearly visible first order diffraction maxima (points on the screen where the amplification of interference has occurred). We mark the maxima with a pencil.
  6. We measure the distance 2y between the two marks. The photo below shows the distance of the first order maxima and the distance between the CD and the laser pointer (e.g. paper).
  
  7. Using the relation (1), where \( \sinα=\frac{y}{\sqrt{l^2+y^2}}\), we can determine the laser wavelength and the grating constant, depending on what we choose as a known variable.

• Sample result

  In an exemplary experiment with l = 25 cm the distance 2y = 18 cm was measured. To calculate sinα we need to know the distance y, which in our case is 9 cm. If we calculate the grating constant, we choose the known variable to be the laser wavelength. During this experiment a green laser with a wavelength λ = 532 nm was used. Then

  \[ b=\frac{λ}{\sinα}.\]

  After substituting correctly converted units we obtain

  \[ b=\frac{5.32\,\cdot10^{-7}}{\frac{0.09}{\sqrt{0.09^2+0.25^2}}}\, \mathrm{m} \doteq 1{,}57\,\cdot10^{-6}\, \mathrm{m} \doteq1570\, \mathrm{nm} \]

  According to the result the rows should be spaced 1570 nm; per 1 mm there would therefore be approximately 637 rows. The stated distance of the rows on a CD is 1600 nm; 625 rows per 1 mm. This value differs by less than two percent of the measured values.

  From the measured values we can also calculate the laser wavelength. We use the grating constant to be b = 1600 nm. The calculation will look like this:

  λ = b sinα.

  \[ \lambda=1.6\,\cdot10^{-6}\cdot \frac{0.09}{0.09^2+0.25^2 }\,\mathrm{m} \doteq 542\,\mathrm{nm}. \]

  The wavelength of the laser is λ = 532 nm. The result differs by 10 nm, i.e. by less than 2 %.

• Technical Notes

  • When you work with a laser pointer you must follow the safety rules.
  • This experiment should be observed from a direction perpendicular to the laser beam to avoid visual impediment.
  • Instead of a plastic CD box, the CD can be attached to the mat by a plasticine.

• Pedagogical notes

  • In these calculations we use known values. The wavelength of the emitted light is stated on the laser pointer. The distance of the rows on a CD is 1600 nm.

  • We can perform this experiment also with a DVD with the row distance 740 nm.

  • Furthermore, we can show the students that if you point a laser on a DVD, the first order maxima are more distant than in the experiment with a CD.

• Link to related task

  The calculation of a grating constant in this experiment is based on the experimental data. A more detailed calculation of the grating constant is described in the task DVD as an Optical Grating.