Collection of Physics Experiments

Winding of a Coil

Experiment number : 1762

• Goal of experiment

  This experiment shows what a winding of a coil is in an unusual way. It also serves for practicing the equation for transformation ratio.

• Assignment

  Determine the number of turns of the secondary coil, so that the voltage induced in the transformer is 900 mV, provided that the primary coil has 60 turns and the primary voltage is 12 V.

• Theory

  The transformer consists of two coils connected by a core. The coil connected to the power supply is called primary coil; the coil, to which the appliance is connected, is called secondary coil (see the figure). In our case, the appliance is a voltmeter.

  

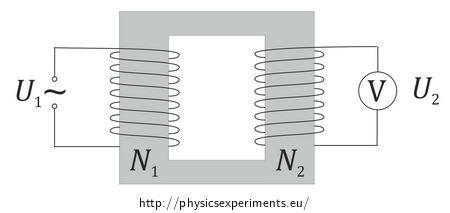
  The number of turns of primary (resp. secondary) coil is denoted N₁ (resp. N₂), primary (resp. secondary) voltage is denoted U₁ (resp. U₂).

  The voltage induced on the secondary coil is determined by so-called transformation ratio:

  \[ \frac{U_1}{U_2}=\frac{N_1}{N_2}.\tag{1}\]

  Since the assignment of the task is to count the number of turns of the secondary coil, we adjust the equation (1):

  \[ N_2=\frac{U_2}{U_1}N_1.\tag{2}\]

  If we substitute the given values into the relation above, we obtain the number of turns.

• Tools

  • laminated U and I core
  • AC voltage source 12 V
  • coil with 60 turns
  • voltmeter
  • circuit connecting wires

• Procedure

  1. According to relation (2) determine the number of turns of the second coil.
  2. Place the coil with 60 turns on the closed laminated core and connect it to the AC voltage source 12 V.
  3. Wind the number of turns you have determined on the secondary side of the transformer; connect the ends of the wire to voltmeter.
  4. Turn the voltage source on and make sure the secondary voltage corresponds to the assignment.

  
  

  

• Sample result

  This task is more difficult than it seems. The calculation gives us the answer that the secondary coil should have 4.5 turns. This can be seemingly achieved by winding the last turn around the core “only half way”. Unfortunately, however, this turn acts as a whole turn – it closes through the voltmeter. 4.5 turns thus cannot be wound in such manner. Therefore the voltmeter will indicate less than the given value (if we wind 4 turns) or more (if we wind 5 turns).

  With these specified parameters without further modifications this task is impossible to solve. There are several ways you can modify the arrangement to achieve the given parameters:

  • Utilize the scatter around the transformer core and wind the wire around the whole transformer, so that the induced voltage is 0.9 V.
  • Partly open the core.
  • Change the size of the secondary part of the core.

• Pedagogical notes

  The assignment is deliberately written so that the task is impossible to solve. Due to the escalation, the students can realize more easily that it is impossible to wind “half a turn”. The students can simultaneously test that the wire moving around the core (increasing the surface of the turn) does not change the induced voltage and that it does not depend on the size of the turn.

  However, the teacher should be aware that the problem is impossible to solve, and work with students’ reactions delicately. He or she should also explain his or her intentions in giving them this task. Advanced students can independently try to figure out how to fulfil the task – how to adjust the arrangement of the experiment, so that the secondary voltage is 900 mV.