Experimental determination of Specific Heat of Water

Experiment number : 1767

Goal of experiment
The goal of this experiment is to experimentally determine the specific heat capacity of water and compare it with the table value.
Theory
General information about specific heat capacity can be found in the task Comparing Specific Heat of Water and Vegetable Oil, Theory. Let us note that if we know the specific heat capacity c of a substance of mass m, which is heated (cooled) by Δt, the heat Q supplied to (taken out of) the substance can be expressed as:
\[Q\,=\,cm\Delta t,\tag{1}\]
In this experiment, the water is heated by electric current passing through a heating coil. If such a coil is connected to a voltage source U and electric current I passes through it in time τ electric work W_e is performed in the coil and it is described as:
\[W_\mathrm{e}\,=\,UI\tau\tag{2}\]
If we heat the water using an alternating current, then U and I are the effective values.

When the current passes through the heating coil, the coil warms up and transfers heat to the water and the inner container of the calorimeter (the outer container is insulated from the inner one by polystyrene; therefore we do not have to consider the heating of the outer container of the calorimeter). Because the law of conservation of energy applies, the electrical work done on the coil W_e must be equal to the total supplied heat; mathematically written:
\[ W_\mathrm{e}\,=\,Q_\mathrm{w} + Q_\mathrm{c} \tag{3}\]
where Q_w is the heat supplied to the water and Q_c is the heat supplied to the calorimeter. On the basis of the equation (1) we can now substitute for the heats in the equation (3) and we obtain
\[ W_\mathrm{e}\,=\,c_\mathrm{w}m_\mathrm{w}\Delta t\,+\,c_\mathrm{c}m_\mathrm{c}\Delta t\tag{4}\]
where c_w anf c_c are the specific heat capacity of water, resp. of the material from which the inner container of the calorimeter is made, and m_w a m_c is the mass of water, resp. of the inner container of the calorimeter. The temperature increase Δt is the same for water and calorimeter because these objects are in thermal equilibrium, unless they are heated extremely quickly. Finally, all that remains is to substitute from the equation (2) into the equation (4) and evaluate the specific heat capacity of water:
\[c_\mathrm{w}\,=\,\frac{W_\mathrm{e}\,-\,c_\mathrm{c}m_\mathrm{c}\Delta t}{m_\mathrm{w}\Delta t}\,=\,\frac{UI\tau\,-\,c_\mathrm{c}m_\mathrm{c}\Delta t}{m_\mathrm{w}\Delta t}\tag{5}\]
The relation (5) gives us clear information which variables need to be determined when calculating the specific heat capacity.
Tools
Calorimeter with a heating coil (Fig. 1), ammeter and voltmeter (or two multimeters), thermometer (preferably with connection to a computer), AC voltage source, balance.
Procedure
1. Measure 100 g of water (mass m_w). Then measure the mass of the inner container of the calorimeter (mass m_c) and pour the 100 g of water into it (i.e. approximately 100 ml).
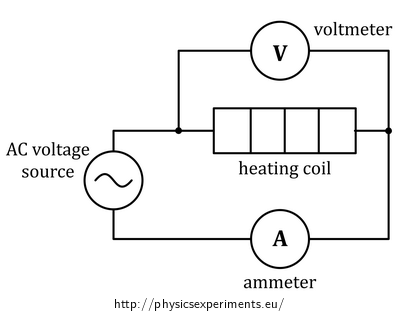
2. Connect the heating coil into the circuit with the AC voltage source, ammeter and voltmeter (the circuit diagram is shown in Figure 2, the arrangement of the experiment is shown in Figure 3).
1. With the power supply still off, choose such a combination of voltage and resistance of the coil, so that the electrical current in the circuit is about 2 A (for example in the sample measurement it is 24 V and 12 Ω).
2. Before turning the power supply on, measure the temperature of water in the calorimeter; leave the thermometer in the calorimeter during the whole measurement.
3. Turn on the power supply and at the same begin to measure the time of the heating. Also take notes of the voltage and current values.
4. After about 3 or 4 minutes turn the power supply off, quickly stir the water with a stirrer and read the final temperature of the water. Do not forget to write down the time of heating τ.

Sample result

The following table summarizes seven exemplary measurements performed for various combinations of heating time τ, mass of water m_w and temperature difference Δt. The remaining parameters were unchanged in all measurements, namely:

\(c_\mathrm{c}\,=\,896\,\mathrm{J{\cdot}kg^{−1}{\cdot}K^{-1}}\)

\(m_\mathrm{c}\,=\,0.031\,\mathrm{kg}\)

\(U\,=\,25.9\,\mathrm{V}\)

\(I\,=\,1.85\,\mathrm{A}\)

The specific heat capacity was calculated according to the equation (5).

Measurement no.	m_w / kg	τ / s	Δt / °C	c_w / J·kg⁻¹·K⁻¹
1	0.110	180	17.0	4360
2	0.103	200	19.8	4440
3	0.110	200	18.8	4380
4	0.108	190	18.5	4310
5	0.104	210	20.6	4430
6	0.095	195	20.4	4530
7	0.111	185	17.0	4440

The average value of the specific heat capacity of water is \(c\,=\,(4410\,\pm\,70)\,\mathrm{J{\cdot}kg^{−1}{\cdot}K^{-1}}\), the table value is 4180 J·kg⁻¹·K⁻¹; the measurement error is about 5 % of this value.

Technical notes
- Before recording the final temperature of the water, it is necessary to stir the water in the calorimeter; otherwise we obtain very distorted results. Based on the experience of the author, it is recommended to stir the water during the last minute of the experiment
- Using a thermometer connected to a computer leads to more accurate results, especially in the case of a short time of measurement, when the temperature increase is small.
Pedagogical notes
- The equation (3) represents an ideal case that does not consider for example heating of the surrounding air and polystyrene insulation of the calorimeter, condensation of the water on the bottom part of the lid and other heat losses. Therefore, in practice we obtain an inequality:
  \[W_\mathrm{e}\,\gt\,Q_\mathrm{w}\,+\,Q_\mathrm{c}\]
  In other words, the efficiency of converting the electrical energy into heat is not 100 %. For this reason the calculated specific heat capacity is systematically greater than the table value of 4180 J·kg⁻¹·K⁻¹.
- More proficient students can object that intensive stirring of the water in the calorimeter can cause a temperature increase of water, because mechanical work is performed. This thought is correct and deserves acknowledgement, although the effect of such heating on the result can be neglected. If we want to convince the students, we can let them estimate the mechanical power performed when stirring and compare it with the electrical power of the heating coil.
Link to a related problem
A quantitative problem that works with the calorimetric equation is Heating of water in electric kettle.

Difficulty level: From Upper secondary level