Ice Regelation
Experiment number : 2256
Goal of Experiment
This experiment shows and describes ice regelation, a phenomenon in which a string with weight passes through a block of ice. After the string passes through the ice, the ice remains in one piece.
Theory
A block of ice taken out from the freezer heats up until it reaches the temperature of 0 °C. The ice gradually melts from the surface by which it slowly absorbs the latent heat of melting. The surface of the ice is covered with a very thin layer of water, with the temperature at the ice/water interface remaining at 0 °C.
The melting temperature of ice decreases with increasing pressure. Underneath the string, the pressure causes the melting point of the ice to drop below 0 °C (in our conditions it was about −0.48 °C; see Comment section). Since the ice temperature is still 0 °C, the ice just below the string melts, and the string moves down in the water that is formed by melting. While the ice melts, it receives the latent heat of melting from the area around the string and the temperature of this area drops well below 0 °C. This causes the water that is now above the string and no longer under increased pressure to freeze again. This will release the latent heat of melting and raise the temperature around this area again to 0 °C. These steps are repeated until the string completely passes through the whole block of ice.
Equipment
Plastic bottle
Water
Knife
Metal guitar string (E1 string is the most suitable for this experiment)
Bucket
Weight

Procedure
Fill the plastic bottle with water and let it freeze.
After a few hours, cut the bottle and remove the ice.
Place two tables side by side so that there is a gap about 10 cm wide between them. Place the ice on these tables so that the centre of the block is over the gap. It is advisable to lay the ice on a towel.
Lead a guitar string over the ice and attach it to a bucket so that its bottom hangs about 30 cm above the floor. Put 6-7 kg of weights in the bucket.
Watch the string slowly pass through the ice and the ice above the string freeze again.
Sample Result
In this experiment we used a guitar string with a diameter of 0.24 mm and a kevlar fibre with a diameter of 0.30 mm. Regelation with kevlar fibre lasted longer than with a guitar string, not only because of the higher thermal conductivity of the string, but also because the kevlar fibre had a larger diameter than the guitar string. The pressure caused by the kevlar fibre was therefore lower than the pressure caused by the guitar string, and the melting point below the kevlar fibre was therefore higher than the melting point below the guitar string.
Technical Notes
When preparing ice, do not fill the plastic bottle to the brim. The volume of water increases during freezing, and if you fill it to the brim, it could burst.
If you are going to try this, it is better to remove the ice from the freezer about 20 min – 1 hour in advance. The ice will have a higher temperature than it had when it was removed from the freezer and the regelation would be faster. When shooting the video, we took the ice out approximately 30 minutes before the experiment and it took 10 minutes for the guitar string to pass through the ice.
Pedagogical Notes
If you show this experiment with both a guitar string and a kevlar fibre, both strings should have approximately the same diameter so that the experiments would be conducted under similar conditions. The guitar string we used was 0.24 mm in diameter, the kevlar fibre was 0.30 mm in diameter.
Comment – Melting Point of Ice at Higher Pressure
Notation
m = 6.5 kg mass of weight suspended on string d = 2.4·10−4 m guitar string diameter l = 5.6·10−2 m diameter of ice block at the point where guitar string causes pressure Table values
lm = 334 kJ·kg−1 specific latent heat of melting ρW = 999,8 kg·m−3 water density at 0 °C ρI = 916,8 kg·m−3 ice density at 0 °C T = 373.15 K melting point of ice 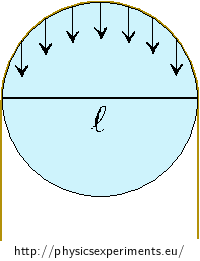
The picture shows a cross-section of ice on which a guitar string is suspended. The string presses perpendicularly to the ice, therefore we only consider the projection of the pressure forces exerted by the string into the vertical direction.
The length l decreases as the string cuts through the ice and the pressure increases. Next, we calculate the change in the melting point at the beginning of regelation.
We use the Clausius–Clapeyron equation, which describes the change of pressure with temperature during the phase transition. This equation has the form of
\[\frac{dp}{dT} = \frac{L_\mathrm{m}}{TΔV},\]where Lm is the latent heat of melting, T is the melting point of ice and ΔV is the change in volume after the ice melts.
We want to know how the melting point of ice changes if a string presses on the ice. The temperature change can be derived from the relation
\[dT = dp\frac{TΔV}{L_\mathrm{m}}.\tag{1}\]To calculate the change in melting point, we first need to find out the change in pressure dp on ice if we hang a string with a weight on it. The pressure p caused by the string on ice is calculated as
\[p = \frac{F}{S} = \frac{mg}{ld},\]where m is the mass of the weight suspended on the string, l is the diameter of the ice block at the point where the string causes pressure and d is the string diameter. We insert given values into the relation
\[p = \frac{6.5·9.8}{5.6·10^{−2}·2.4·10^{−4}} \mathrm{Pa}.\]The pressure caused by the string with a suspended weight is approximately equal to
\[p \dot{=} 4.74·10^{6} \mathrm{Pa}.\]The string therefore causes the pressure to increase by p. The change in pressure dp on ice will thus be
\[dp \dot{=} 4.74·10^{6} \mathrm{Pa}.\]We also need to know the change in volume when the ice melts. We can determine it as the difference between the volume of water VW and the volume of ice VI of the same mass of 1 kg
\[ΔV = V_\mathrm{W}−V_\mathrm{I} = \frac{m_\mathrm{W}}{ρ_\mathrm{W}}−\frac{m_\mathrm{I}}{ρ_\mathrm{I}}.\]Now we can substitute into (1) and determine the change of melting point of ice
\[dT = dp\frac{TΔV}{l_\mathrm{m}} = p\frac{T(\frac{m_\mathrm{W}}{ρ_\mathrm{W}}−\frac{m_\mathrm{I}}{ρ_\mathrm{I}})}{L_\mathrm{m}}.\]After substituting given values we get
\[dT \dot{=} 4.74·10^{6}\frac{373.15·(\frac{1}{999.8}−\frac{1}{916.8})}{3.34·10^{5}} °\mathrm{C}\] \[dT \dot{=} −0.48 °\mathrm{C}.\]Under the conditions in which our measurements took place, the melting point of the ice under the weighted string dropped by approximately 0.48 °C.