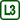Two soap bubbles connected with a tube
Experiment number : 2081
Goal of experiment
We show in this experiment, what happens to two soap bubbles of different diameters when we connect their insides (we let the air to flow from one bubble into the other).
In this way, we demonstrate the dependence of Laplace pressure below a curved surface of a liquid on the radius of the surface.
Theory
The diameters of the bubbles will change (air will flow from one bubble to the other) only if there is a higher pressure inside one of the bubbles than in the other. The air will then flow from the bubble with higher pressure into the other one.
The pressure inside both bubbles is given by the atmospherical pressure, the equlibrium pressure of the water vapor evaporated from the membrane of the bubble and by the Laplace pressure of the curved bubble membranes. The atmospherical pressure and the vapor pressure inside both bubbles is the same.
The Laplace pressure occurs below curved surfaces of liquids as a result of surface tension. One can easily observe its action as it defines the shape of bubbles, droplets or liquid surfaces in capillary tubes. We denote it pL.
The Laplace pressure inside a bubble is given as:
\[p_\mathrm{L} = \frac{4σ}{r},\]where σ is the surface tension of the liquid and r is the radius of the bubble.
The Laplace pressure is inversely proportional to the bubble radius: it is higher inside the smaller bubble than in the larger bubble. The air thus must flow from the smaller bubble into the larger one.
A solved task with a derivation of the formula for Laplace pressure is found here: Two connected soap bubbles.
Equipment
glass tube with a three-way valve (or two drinking straws or other tubes that can be connected)
beaker
liquid soap or dishwashing liquid

Procedure
Procedure with a glass tube with a three-way valve:
Perpare soapy solution in the beakeer.
Open the valve from the inlet into one end of the tube. Wet this tube end in the soapy solution, blow out a small bubble and close this end of the tube with the valve.
Open the valve from the inlet into the other end of the tube and blow out a larger bubble the same way. Close both tube ends with the valve.
Turn the valve so that it connects the two tube ends (the insides of the bubbles) with the air inlet closed.
Observe what happens to the bubbles.

The procudure is pretty similar with drinking straws:
Wet one straw in the soapy solution, blow out a bubble on its end and close the other end of the straw with a finger.
Blow out a bubble on one end of the other straw and close its other end with a finger.
Connect the closed ends of the straws so that the air can flow between the bubbles.
Observe what happens to the bubbles.
Example of results
Methodical notes
It is good to try out he quality of the soapy solution and working with the three-way valve in advance.
-
A similar experiment can be performed with inflatable balloons, however it presents only an analogy to the bubble experiment.
There is again a higher pressure in the less inflated balloon than in the more inflated balloon. After connecting two differently inflated balloons, the air flows from the smaller one into the larger one, like with bubbles. The pressure inside the balloon again decreases with increasing radius of the balloon. However, the membrane forces that cause the inner pressure in the balloon are not the same as in a bubble.
The bubble membrane consists of molecules of the liquid with a constant spacing – with increasing bubble diameter, more molecules move from the inside of the membrane to its outer and inner surfaces. The liquid on the surface and its surface tension is the same regardless of the bubble diameter.
The balloon membrane is made of rubber – tangled macromolecules that gradually straighten up when inflating the balloon. The tension in the rubber membrane originates in the whole thickness of the rubber sheet, not only in its surface. The surface forces consequently depend on how much the rubber membrane is stretched. The pressure inside the rubber balloon is mathematically analogous to the Laplace pressure but the tension of the rubber membrane depends on the diameter of the balloon in this case.