Absorption of Thermal Radiation by Plastic Filters
Experiment number : 4350
Goal of experiment
The goal of the experiment is to measure how thermal radiation emitted by an object is attenuated when passing through plastic filters.
Theory
The experiment described below is based on thermal imaging camera visualisation. Thermal imaging measurement principle is to detect the radiation emitted by the measured object. If the thermal imaging camera evaluates the intensity of emitted radiation \(I\) \(([I]\,=\,\mathrm{W{\cdot}m^{-2}})\), the surface temperature T of the body with emissivity ε can be estimated using the Stefan-Boltzmann Law:
\[I\,=\,{\epsilon}{\sigma}T^4\tag{1}\]where σ is the Stefan-Boltzmann constant.
Relation (1) is a simplification of the actual situation – firstly, it assumes that the measured object can be modelled by a so-called grey body, i.e. a body with emissivity independent of the frequency of the emitted radiation. Secondly, it neglects the radiation of the atmosphere and own radiation of the thermal camera chip, which are also taken into account and corrected when evaluating the temperature of the measured object.
If the emitted radiation with the initial intensity \(I_0\) passes through a material of thickness d, it is absorbed in the material and its intensity decreases exponentially depending on the thickness of the material according to the relation:
\[I(d)\,=\,I_0e^{-\beta d}\tag{2}\]where β is the so-called absorption coefficient characterizing the material. The relationship (2) is often referred to as Lambert-Beer's law and is more commonly encountered when visible light passes through solutions of various substances.
By substituting relation (2) into relation (1) we obtain the theoretically derived temperature course measured by the thermal imaging camera in the form:
\[{\epsilon}{\sigma}T^4\,=\,{\epsilon}{\sigma}T_0^4e^{-\beta d}\tag{3}\] \[T\,=\,T_0\sqrt[4]{e^{-\beta d}}\tag{4}\]By modifying equation (4), we can then express the expected dependence of the temperature measured by the thermal imaging camera on the thickness of the material d that we insert between the camera and the radiation source:
\[T(d)\,=\,T_0{e^{-{\frac{1}{4}}\beta d}}\tag{5}\]Thus, as in the case of radiation intensity, we should expect an exponential decrease in the measured temperature. In our experiment, we will change the thickness of the material by increasing the number of plastic films placed between the radiation source and the thermal imaging camera.
The aim of the above derivation was to show the fact that the measured temperature value decreases exponentially with the thickness of the absorbing material. Again, this derivation should be taken as idealized – for example, it is clear that as the thickness of the material increases towards infinity, the measured temperature will definitely not approach 0 K as the theoretical model would suggest. Although the intensity of the transmitted radiation will decrease towards zero, the thermal radiation of the absorbing material (in our case, the filters) will become more apparent, causing the exponential describing the temperature course to asymptotically approach room temperature rather than absolute zero.
Equipment
Thermal imaging camera, plastic filters (ca. 10 pieces), object with significantly higher temperature than room temperature.
In the sample experiment, a 60W bulb was used as the object emitting thermal radiation, and its surface almost stabilized at a temperature of about 180 °C after about 10 minutes of operation.
The filters of size approx. 4×5 cm (Fig. 1) were cut out from polypropylene CD/DVD sleeves; similarly e.g. see-though folders could be used. The only requirement for the plastic used is that it should not absorb too much radiation – in such a case, placing one or two filters would prevent the passage of all infrared radiation and furthermore there would be nothing to measure. For this reason, filters made from PET bottles, for example, cannot be used; instead, polypropylene or polyethylene can be recommended.
Procedure
Fix the thermal imaging camera so that it always faces the same spot of the studied object. In the sample measurement, the distance between the camera and the object was approximately 120 cm.
Note the temperature that the camera measures if no filter is placed in front of it.
Insert one filter and record the measured temperature. Repeat the procedure for increasing numbers of filters; it is advisable to measure at least eight values.
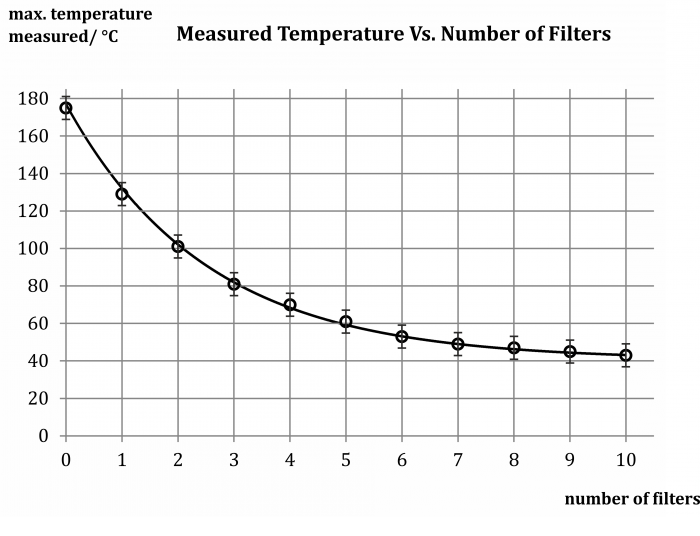
Sample result
The values measured in the sample experiment are shown in the table below:
Number of filters 0 1 2 3 4 5 6 7 8 9 10 Measured temperature (°C) 175 129 101 81 70 61 53 49 47 45 43 These values are graphically processed in the graph in Figure 2 and an exponential dependence is fitted:
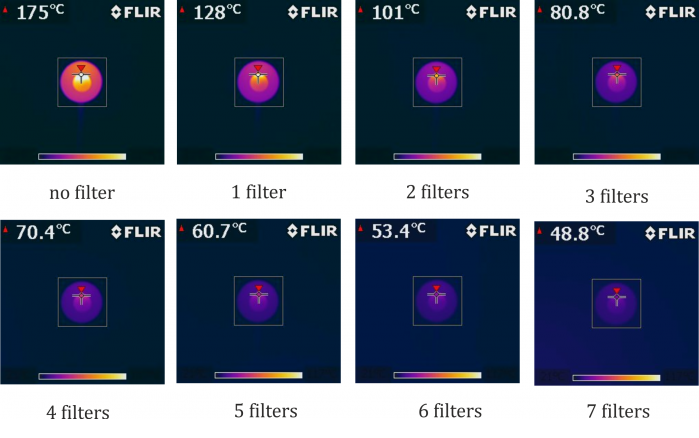
Alternatively, the drop in measured temperature can be expressed directly by images from a thermal imaging camera – see Figure 3.
In this experiment, the FLIR i7 thermal imaging camera was used. The temperature range of the colour scheme was set in the interval of 21 °C and 117 °C, the emissivity was ε = 0.95. The camera worked in the maximum mode, where it always showed the highest temperature measured in the white framed square (hence the vertical axis in the graph above).
Technical notes
If we want to use a light bulb in the experiment as in the sample experiment, we need to leave it on for about 10 minutes before the measurement starts, so that its surface temperature stabilizes. This settling is not perfect even after 10 minutes, but the temperature rise is already so slow that it does not disturb the measured exponential dependence. However, it is certainly not possible to start the measurement shortly after lighting the bulb, when its temperature is still increasing steeply; in general, we need to use a body with an approximately constant surface temperature.
Another way we can implement plastic filters is to use a square of duct tape as the basic unit and gradually increase the thickness of the absorbing material by sticking more and more layers.
Pedagogical notes
To make the experiment even more illustrative, it may be useful to use a study object that does not emit visible light – to make it really clear to the students that what is being detected by the thermal camera and attenuated by the filters is thermal infrared radiation. An object that does not give off visible light and at the same time maintains an approximately constant temperature well above the ambient temperature could be, for example, a kettle with boiling water and an open lid (this ensures that the kettle does not turn off despite the water boiling).
We can discuss with students whether it is a problem that we derived relation (5) for thermodynamic temperature, but the graph in Figure 2 is plotted for Celsius temperature. Students will find quite easily that in the case of a thermodynamic temperature scale, the entire graph would just shift along the vertical axis.
It is necessary to perceive the derived relation (5) really only as a first approximation of the real situation – real thermal imaging cameras work with more complicated mathematical relations, filters reflect part of the radiation etc.
Thermal imaging camera basics - link to PDF
In this experiment, a thermographic measurement is used. The theory of thermography and basic recommendation and procedures that can help you obtain more accurate and undistorted results can be found in Experiments with thermal imaging camera (in Czech only).