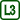Soap Membrane in Frame with Moving Bar
Experiment number : 2126
Goal of experiment
The goal of this experiment is to visualize a surface force that a soap membrane enacts on a moving bar.
Theory – Surface energy and surface force
Surface energy and surface force
Molecules in a surface layer of a liquid have greater potential energy than molecules inside the liquid. This additional potential energy is the surface energy. With increasing surface area of the liquid the surface energy increases. Since the equilibrium state is the state with minimal potential energy, the liquid tries to assume a shape with the smallest surface area in order to achieve equilibrium state. The surface layer of the liquid behaves like a flexible membrane that wants to assume the smallest area.
We can create a soap membrane from a soap solution in a wire frame with a moving bar. The membrane tends to retract to have the smallest surface area. To keep the extended membrane in equilibrium, a force needs to act perpendicular to the membrane. This force is called the surface force and is directly proportional to the length of the membrane surface.
We will be interested in the surface force acting on the moving bar. Due to the fact that the soap membrane in the frame has two surfaces, the size of the surface force Fs with which the membrane acts on the bar is:
\[F_\mathrm{s} =2 σl,\tag{1}\]where σ is the surface tension of the liquid and l is the length of the bar.
The surface force acts on the other parts of the frame, too. However, these are strong enough not to collapse, so the force effect is not shown.
When we suspend the wire frame on a stand, the gravitational force will act perpendicular to the bar. The gravitational force is directly proportional to the mass of the bar and the weight we can hang on the bar.
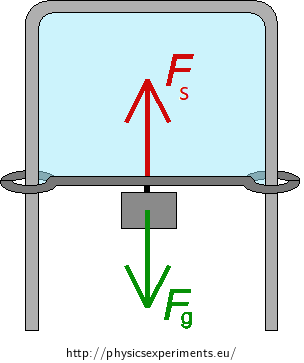
If the gravitational force Fg is smaller than the surface force Fs, the membrane retracts and the bar moves upwards quickly.
If the gravitational force is equal to the surface force, the net force acting on the bar is zero and the bar stays at rest.
If the bar is too heavy or if we hang a heavy weight on it, the gravitational force is greater than the surface force, and the bar moves downwards quickly.
We assume that the bar can move freely and without friction.
Tools
soap water
wire frame with a moving bar
weights that can be hung on the bar (we used a coiled wire as a weight)
laboratory scales (if you want to measure the surface tension of soap water)
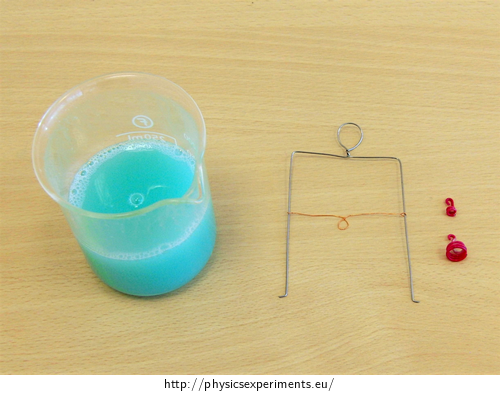
Procedure
Immerse the wire frame into the soap water.
Hang the frame on the stand (or you can just hold it in your hand).
Drag the movable bar downwards to increase the surface of the soap membrane. Then let the bar go and watch the membrane retract.
Drag the bar again to extend the membrane surface and then hang the weights on the bar so that the gravitational force acting on the bar with the weights equals the surface force of the membrane acting on the bar. The bar remains at rest.
Hang a heavier weight on the bar so that it moves downwards.
Sample result
Comment
Calculation of surface tension of soap water
We can measure the length of the bar and weigh the bar and the weights that hold the membrane extended and at rest. From this data we can determine the surface tension of soap water.
Sample result:
length of the bar l = 58 mm = 5.8·10−2 m mass of the bar mb = 0.078 g mass of weights mw = 0.137 g mass of the bar and weight together mb+w = 0.215 g = 2.15·10−4 kg
The bar acts on the membrane with gravitational force Fg
\[F_\mathrm{g} = m_\mathrm{b+w}·g \dot{=}\, 2·10^{−4}·10 = 2·10^{−3} \mathrm{N}.\]The bar is in balance. The membrane must have a surface force Fs of the same size as the gravitational force but in the opposite direction
\[F_\mathrm{s} = F_\mathrm{g}.\]The surface force the membrane acts on the bar is
\[F_\mathrm{s} \dot{=}\, 2·10^{−3} \mathrm{N}.\]Surface force can be calculated according to (1) as
\[F_\mathrm{s} = 2σl.\]From this relationship we express the surface tension
\[σ = \frac{F_\mathrm{g}}{2l}.\]We insert the measured values and calculate the surface tension of soap water
\[σ \dot{=}\, \frac{2·10^{−3}}{2·5.8·10^{−2}} \mathrm{N·m^{−1}}\] \[σ \dot{=}\, 1.7·10^{−2} \mathrm{N·m^{−1}}.\]Soap water we used in our experiment had a surface tension of about 1.7·10−2 N·m−1.
The solved part of the soap membrane can be found here: Soap Film in a Wire Frame with a Movable Crossbar.
Technical notes
If you move the moving bar and the membrane does not shrink, it is possible that the bar is too heavy. For this experiment, it is a good idea to use a bar with as little mass as possible. You can make a suitable bar yourself from a thin wire.
You also need to make sufficiently large eyelets and take care that the bar does not buckle and rub against the frame during the experiment.