Evaporation of Water and Ethanol (with Thermal Imaging Camera)
Experiment number : 1941
Goal of experiment
We will observe the rate of changes in temperature during the evaporation of water and technical ethanol.
Theory
Evaporation, that is a transformation of a liquid into a gas, occurs at every temperature at which the given substance is liquid. The rate of evaporation (which could be defined as a mass of a liquid evaporated in a unit of time) depends on many different parameters – the temperature of the liquid, the pressure of the vapours above its surface, its surface area, the presence of flow on the surface etc. Due to this variety of factors affecting the rate of evaporation, it is probably not an ideal parameter to help us compare different evaporating liquids.
That is one of the reasons why we use a different quantity to compare the willingness of liquids to evaporate, and that is specific heat of vaporization lv, which tells us how much energy is needed to evaporate one kilogram of a liquid. Specific heat of vaporization decreases with increasing temperature. That tells us that hotter liquid needs less heat to evaporate one kilogram of it at a fixed temperature. This intuitively makes sense. For example, while the specific heat capacity of water at 0 °C is 2.50 MJ·kg-1, at 100 °C it is only 2.26 MJ·kg-1. You can learn more about specific heat capacity in the section with the same name at the end of this experiment.
Comparing specific heats of evaporation at an arbitrary temperature, for example 20 °C, is often a problem – the tables usually contain only specific heat of vaporization for boiling temperatures (for example 100 °C for water, 78 °C for ethanol, 357 °C for mercury etc.). Therefore in our experiment we will compare specific heats of vaporization of water and ethanol at their boiling temperatures, even though they are listed at different temperatures (100 °C and 78 °C respectively) and these temperatures are very distant from room temperature at which our experiment is conducted. It will, however, suffice to give us a general quantitative idea.
Tools
Thermal imaging camera, two cups, water and ethanol at room temperature, two straws.
Procedure
We prepare two cups and fill one with water and the other with the same amount of ethanol; both should be at room temperature at the beginning of the experiment. We observe the cups with a thermal imaging camera. We simultaneously submerge identical straws into both cups and take them out after a few seconds. We observe how the temperature of the straws changes.
Sample result
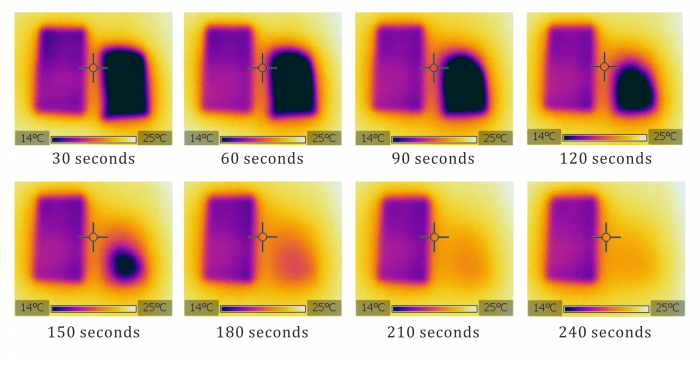
A successful execution of the experiment is shown in the video below. The liquids evaporate from the straws and take the heat of vaporization away from them. As a result, the temperature of both straws then decreases. The decrease is more significant in the case of the straw submerged in ethanol.
A thermal imaging camera FLIR i7 was used in the making of this video. The temperature scale of colours was chosen between 12 °C až 23 °C, emissivitz ε = 0.95. The video was slowed down twice.
Technical notes
To make the measurement really conclusive, it is advisable to have both liquids ready in their cups long enough before the experiment so that they are in thermodynamic equilibrium with their surroundings.
We can use other insulators instead of straws, but the experiment works reliably with straws.
Pedagogical notes
At first sight, the result of the experiment puts us into a remarkable conflict. We have just shown that the straw submerged in technical ethanol cooled down more than the straw submerged in water. That means ethanol took away more heat. However, if we look into the tables, we find out that specific heat of vaporization of ethanol (879 kJ·kg-1) is about three times less than that of water (2257 kJ·kg-1) – it is water that should take more heat away from the straw (if we assume approximately same amounts of water and ethanol stuck to the straws).
If a brighter student asks this question, we can follow it up with another debate – for example by asking about ways in which evaporation of ethanol is different from evaporation of water. We will come to the conclusion that ethanol evaporates much more intensely – its whole volume evaporates in a relatively short amount of time, therefore its surroundings do not have time to compensate for the sudden decrease in temperature that we then measure. On the other hand, water evaporates slowly, so the decrease in temperature caused by its evaporation is compensated for by its surroundings – the temperature of water then never reaches as low as in the case of technical ethanol, but the total heat absorbed by the evaporating water will indeed be greater than the heat absorbed by the same mass of ethanol. In reality, there is no conflict between theory and our experiment.
The explanation above can be easily proven experimentally – all we have to do is observe both straws for several minutes after taking them out of the liquids. All of the ethanol usually evaporates in this time and the straw submerged in it quickly returns to room temperature, whereas the more slowly evaporating water still cools down the other straw. This phenomenon is shown for example in Fig. 1 – two identical pieces of paper were used here instead of straws – the left one was submerged in water and the right one in ethanol.
More about specific heat of vaporization
In the text above we spoke about how specific heat of vaporization is a characteristic quantity of liquids at a given temperature and that it indicates the heat needed for 1 kg of this liquid to evaporate. This heat taken by the liquid from its surroundings has a dual character – a part of it is used to increase the internal energy of the system (internal specific heat of vaporization lvi), but a part of it is also used for the work the gas does while increasing its volume from the volume of the liquid (external specific heat of vaporization lve). The external part is significantly smaller than the internal part. Internal, external and total heats of vaporization at different temperatures are shown as an example in the table below. (Pressure of course increases so that water can remain liquid.)
\(\mathrm{temperature\,/\,K}\) \(l_{\mathrm{vi}}\,/\,\mathrm{kJ{\cdot}kg^{-1}}\) \(l_\mathrm{ve}\,/\,\mathrm{kJ{\cdot}kg^{-1}}\) \(l_\mathrm{v}\,=\,l_\mathrm{vi}\,+\,l_\mathrm{ve}\,/\,\mathrm{kJ{\cdot}kg^{-1}}\) 273.15 2374 126 2500 373.15 2086 170 2256 473.15 1744 198 1942 573.15 1233 171 1404 647.10 0 0 0 The data in the table correspond with the previously mentioned knowledge that specific heats of vaporization decrease with increasing temperature. They reach zero at a critical temperature where the difference between water and its saturated vapour disappears: lv = 0. That is also visible in the table above – for water, this critical temperature is approx. 374 °C (approx. 647 K) at pressure equal to 22.14 MPa.